Chapter 2 Code

We’ll use Python’s NumPy library in what follows, as well as Matplotlib for plotting.

import numpy as np
import matplotlib.pyplot as plt

Bisection

Here’s an implementation of the bisection algorithm. We will test it on this function:

f = lambda x: np.sin(4 * (x - 1/4)) + x + x**20 - 1

The implementation:

M = 1000
ϵ = 1e-8
α, β = 0, 1

    
i = 1
a, b = α, β
while i <= M:
    c = (a + b) / 2
    if abs(f(c)) < ϵ:
        print(c)
        break
    i += 1
    if f(a) * f(c) < 0:
        b = c
    else:
        a = c
        
if i > M:
    print("Failed to converge.")

0.408293504267931

User Defined Functions

Here’s the basic implementation of the function \(\tau\).

def tau(z, S, phi):
    """
    Evaluates the function tau(z) given data S, phi, where
    S and phi are assumed to be arrays.
    """
    a = 0
    for i, x in enumerate(S):
        b = a + phi[i]
        if a < z <= b:
            return x
        a = b

Here’s a more efficient implementation.

def tau(z, S, phi):
    i = np.searchsorted(np.cumsum(phi), z)
    return S[i]

And here’s a closure that generates the function \(\tau\).

def tau_factory(S, phi):
    Φ = np.cumsum(phi)
    
    def tau(z):
        i = np.searchsorted(Φ, z)
        return S[i]
    
    return tau

We generate a function \(\tau\) that acts on \(z\) alone by calling the function factory:

phi = 0.2, 0.5, 0.3
S = 0, 1, 2
tau = tau_factory(S, phi)

tau(0.1)  # Should be 0

0

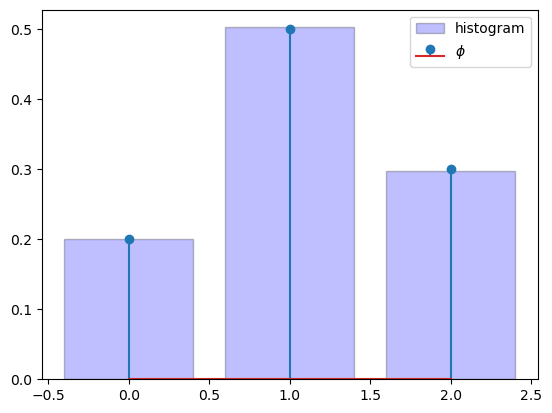
All of these functions work as expected. To illustrate, here \(\tau\) is used to generate draws from a given distribution \(\phi\).

size = 100_000

draws = np.empty(size)
for j in range(size):
    W = np.random.uniform()
    draws[j] = tau(W)
    
# Compute fraction of draws with each possible value
frequency = [np.mean(draws==j) for j in S]
    

Let’s check that the empirical frequency approximately coincides with the probabilities in \(\phi\).

fig, ax = plt.subplots()

ax.bar(S, frequency, 
       edgecolor='k',
       facecolor='b',
       alpha=0.25, 
       label="histogram")

ax.stem(S, phi, label='$\\phi$')

ax.legend()

plt.show()

Object Oriented Programming

Here’s a class that implements the function \(\tau\) as a method, as well as a method to generate draws from \(\phi\).

class Tau:
    
    def __init__(self, S, phi):
        self.S = S
        self.Φ = np.cumsum(phi)
    
    def tau(self, z):
        i = np.searchsorted(self.Φ, z)
        return self.S[i]
    
    def draw(self):
        W = np.random.uniform()
        return self.tau(W)

tau = Tau(S, phi)

for i in range(5):
    print(tau.draw())

0
2
0
0
1